Causal Bounds for Observational Data with Pure Mediators

Uriah Finkel

Causal Question

What are the bounds on the Individual Treatment Effect (ITE) of smoking 🚬 vs. not smoking 🚭 on COPD 🫁, given TAR as a pure mediator ⚫

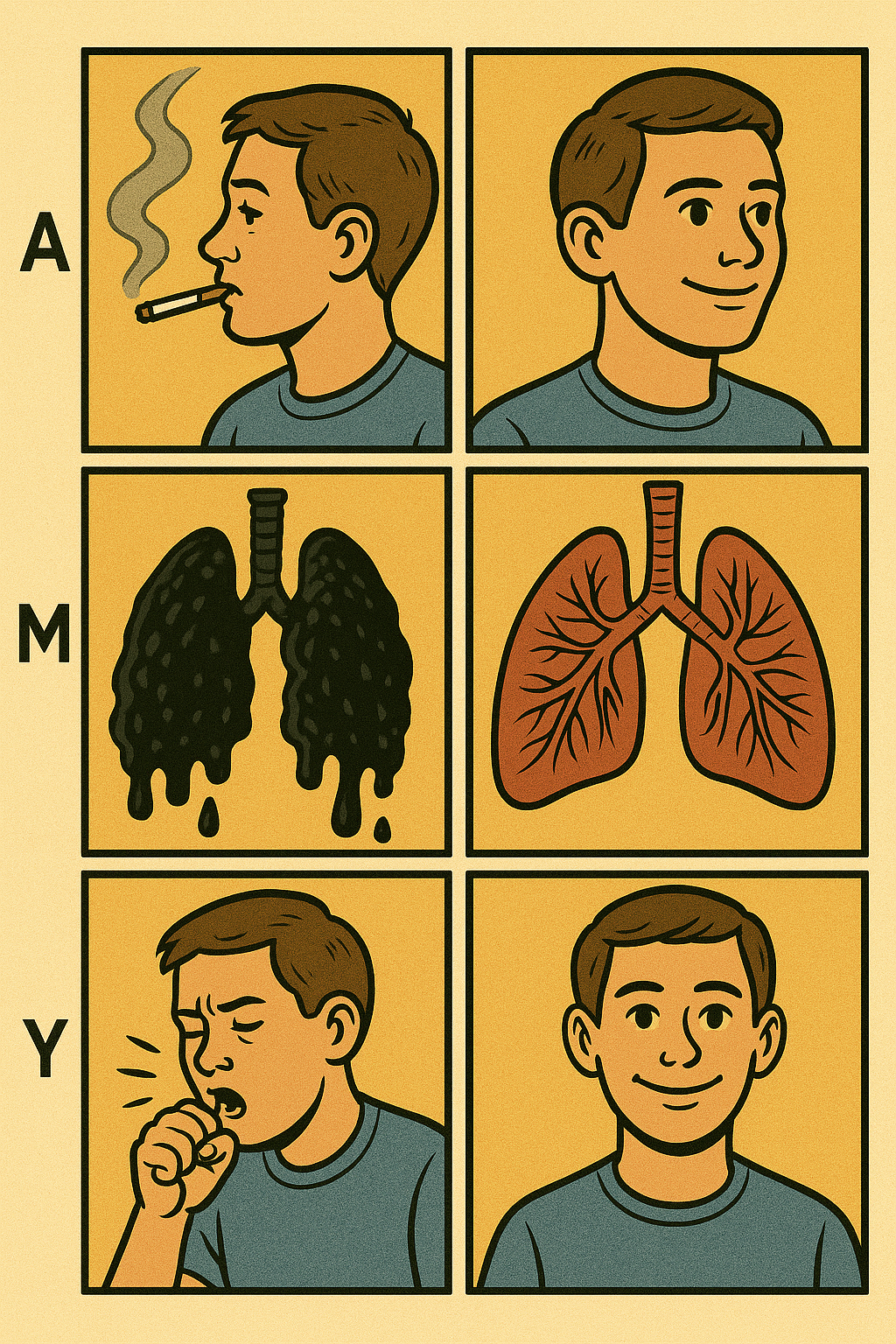
flowchart LR
    classDef smoker fill:#F5F2EB,stroke-width:2px,color:#001F3F;
    classDef tar fill:#F5F2EB,stroke-width:2px,color:#001F3F;
    classDef copd fill:#F5F2EB,stroke-width:2px,color:#001F3F;

    A["Smoking<br>🚬<br><br><span style='font-size:28px; font-weight:900;'>A</span>"]:::smoker --> 
    B["TAR<br>⚫<br><br><span style='font-size:28px; font-weight:900;'>M</span>"]:::tar

    B:::tar --> 
    C["COPD<br>🫁<br><br><span style='font-size:28px; font-weight:900;'>Y</span>"]:::copd

    linkStyle 0 stroke:#001F3F,stroke-width:2px
    linkStyle 1 stroke:#001F3F,stroke-width:2px

😇 God-Given Counterfactual Data

  • By God-Given knowledge we have access to the true counterfactual outcomes for each individual for smoking 🚬 and for not smoking 🚭. The potential outcomes are by definition different for Responders.

\[ \text{PNS} = \text{p( Y=1 | do(A=1), Y=0 | do(A=0) )} = \frac{1}{4} \]

😇 God-Given Counterfactual Data

  • By God-Given knowledge we have access to the true counterfactual outcomes for each individual for smoking 🚬 and for not smoking 🚭. The potential outcomes are by definition different for Responders.

  • In case of pure mediation, the potential outcomes of the mediator must be different as well: In other words smoking cause COPD only through TAR.

\[\small{ \text{PNS} = \text{p( Y=1 | do(M=1), M=1 | do(A=1), Y=0 | do(M=0), M=0 | do(A=0) )} = \frac{1}{4} }\]

😈 Observed Data

In real life we can analyse only the observed outcomes and observed mediators, so we can never know the true Individual Treatment Effect. But fortunately, we can use Causal Bounds taking modifiers into consideration.

Population Level Bounds

Bounds PNS

\[ 0 \le \text{PNS} \le\]

  • In order to bound PNS we need to count the possible proportion of Responders:

Bounds PNS

\[ 0 \le \text{PNS} \le \frac{4}{16} +\]

  • In order to bound PNS we need to count the possible proportion of Responders:

  • The total number of observed non-events without treatment and without TAR, they might be Responders or Immuned.

Bounds PNS

\[ 0 \le \text{PNS} \le \frac{4}{16} + \frac{6}{16}\]

  • In order to bound PNS we need to count the possible proportion of Responders:

  • The total number of observed non-events without treatment and without TAR, they might be Responders or Immuned.

  • The total number of observed events with treatment and with TAR, they might be Responders or Lost-Causes.

Bounds PNS

\[ 0 \le \text{PNS} \le \frac{11}{16} \] Now we know the bounds of the PNS.

It resonates with our true “God-Given” PNS:

\[ 0 \le \text{PNS} = \frac{4}{16} \le \frac{10}{16} \]